|
Как
нужно вычислять
Школьники
привыкли к точным вычислениям. Это иногда приводит к ненужному усложнению
расчета, делает его долгим и трудным. Обиднее всего, если в
конце приходится округлять результат и отбрасывать много лишних
цифр.
Чтобы
избежать потерь времени, полезно заранее, до получения
ответа, оценить погрешность, с которой он будет вычислен. В пределах
этой погрешности можно округлять некоторые числа в промежуточных
расчетах. Например, если нужно умножить 16 на 5987 и
известно, что результат будет иметь погрешность не менее 5%, то можно
умножать 16 на 6000 (это гораздо легче, а ошибка
округления составляет около 0,2% и не искажает результат).
При
вычислении погрешностей излишняя точность просто мешает. Например,
если ширина прямоугольника (17,6±0,1) м, а длина
(46,4±0,2) м, то относительная погрешность вычисления площади
равна 0,1/17,6+0,2/46,4. Если приводить дроби к общему
знаменателю, получится величина 51/5104, которую потом придется
умножать на величину площади, чтобы получить абсолютную
погрешность. Это долго и не нужно. Грубо оценить погрешности можно так:
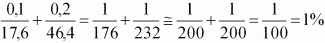
Более
точное вычисление: 0,57% +0,43% = 1% (тот же результат). Величина
площади 17,6·46,4=816,64 м
2
имеет погрешность 8 м
2,
поэтому результат можно округлить до (817±8) м
2.
Значит, сотые доли квадратного метра можно было не
вычислять, но десятые доли были нужны для правильного округления (не
зная их, мы получим (816±8) м
2,
что,
впрочем, тоже не очень плохо при таких погрешностях).
Для
малых величин 0<
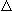 <<1
справедливы следующие приближенные равенства: <<1
справедливы следующие приближенные равенства:
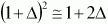 (12) (12)
 (13) (13)
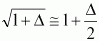 (14) (14)
 (15) (15)
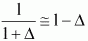 (16) (16)
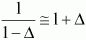 (17) (17)
Погрешности
всех этих равенств имеют порядок
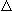 2
это очевидно в (12) и (13). То есть если 2
это очевидно в (12) и (13). То есть если
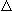 ≅1%,
то ошибка, которую вносят упрощенные вычисления по формулам
(12)—(17), не превышает 0,1%. ≅1%,
то ошибка, которую вносят упрощенные вычисления по формулам
(12)—(17), не превышает 0,1%.
Пример
расчета.
 .
Проверим,
сколь велика ошибка вычислений: 9,92 = (10 – 0,1)2 = 102
– 2·10-0,1+0,12 =100—2+0,01==98,01. Ошибка меньше, чем
0,1%. .
Проверим,
сколь велика ошибка вычислений: 9,92 = (10 – 0,1)2 = 102
– 2·10-0,1+0,12 =100—2+0,01==98,01. Ошибка меньше, чем
0,1%.
Выводы.
Заранее оценив погрешность результата, можно облегчить
вычисления.
|